Problem Description#

Find a point such that the total distance from all other points to it is minimized.

The calculation method for the total distance is: the sum of (each point’s population multiplied by its distance to the target point).

Note! This problem has no edge weights! Only node weights (I stumbled here the first time [facepalm]).

Approach#

There are two methods: brute force and rerooting DP.

The brute force method is straightforward. Since $n$ is small, directly traverse each node from $1$ to $n$ as the root, perform a DFS to calculate the total distance, and take the minimum value.

Rerooting DP involves first performing a DFS to calculate the total distance with node $1$ as the root, then performing another DFS to calculate the total distance with other nodes as the root, and finally taking the minimum value.

So, what is the state transition equation?

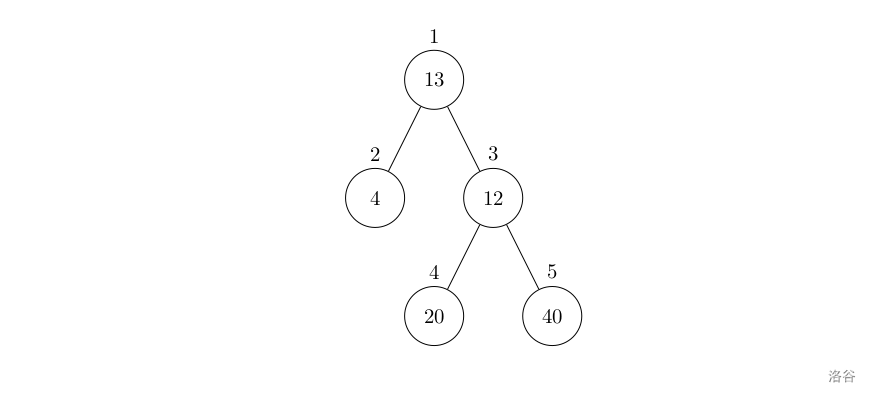
Look at the graph in the problem. If the hospital is moved to node $3$, doesn’t it mean that nodes $1$ and $2$ on the left have to travel farther, while nodes $3$, $4$, and $5$ on the right have to travel less?

Thus, the state transition equation can easily be derived as:

$f[v] = f[u] + size[1] - size[v] - size[v]$

Done!

Code#

1
// Brute force solution
2
#include <iostream>
3
#include <vector>
4
#include <algorithm>
5
using namespace std;
6
vector <int> wth[105];
7
int ans = 1e9, cnt[105], hz[105];
8
int a[105];
9
void dfs(int now, int f, int dep, int rt)
10
{
11
    cnt[now] = hz[now];
12
    a[rt] += hz[now] * dep;
13
    for(auto v : wth[now])
14
    {
15
        if(v == f)
16
        {
17
            continue;
18
        }
19
        dfs(v, now, dep + 1, rt);
20
        cnt[now] += cnt[v];
21
    }
22
}
23
int main()
24
{
25
    int n;
26
    cin >> n;
27
    for(int i = 1; i <= n; i++)
28
    {
29
        int u, v, w;
30
        cin >> w >> u >> v;
31
        hz[i] = w;
32
        if(u != 0)
33
        {
34
            wth[i].push_back(u);
35
            wth[u].push_back(i);
36
        }
37
        if(v != 0)
38
        {
39
            wth[i].push_back(v);
40
            wth[v].push_back(i);
41
        }
42
    }
43
    for(int i = 1; i <= n; i++)
44
    {
45
        dfs(i, 0, 0, i);
46
        ans = min(ans, a[i]);
47
    }
48
    cout << ans;
49
    return 0;
50
}

1
// Rerooting DP solution
2
#include <iostream>
3
#include <vector>
4
#include <algorithm>
5
using namespace std;
6
vector <int> wth[105];
7
int ans = 1e9, cnt[105], hz[105];
8
int a[105];
9
void dfs(int now, int f, int dep)
10
{
11
    cnt[now] = hz[now];
12
    a[1] += hz[now] * dep;
13
    for(auto v : wth[now])
14
    {
15
        if(v == f)
16
        {
17
            continue;
18
        }
19
        dfs(v, now, dep + 1);
20
        cnt[now] += cnt[v];
21
    }
22
}
23
void dfs2(int u, int f)
24
{
25
    if(u != 1)
26
    {
27
        a[u] = a[f] + (cnt[1] - cnt[u]) - cnt[u];
28
    }
29
    ans = min(ans, a[u]);
30
    for(auto v : wth[u])
31
    {
32
        if(v == f)
33
        {
34
            continue;
35
        }
36
        dfs2(v, u);
37
    }
38
}
39
int main()
40
{
41
    int n;
42
    cin >> n;
43
    for(int i = 1; i <= n; i++)
44
    {
45
        int u, v, w;
46
        cin >> w >> u >> v;
47
        hz[i] = w;
48
        if(u != 0)
49
        {
50
            wth[i].push_back(u);
51
            wth[u].push_back(i);
52
        }
53
        if(v != 0)
54
        {
55
            wth[i].push_back(v);
56
            wth[v].push_back(i);
57
        }
58
    }
59
    dfs(1, 0, 0);
60
    dfs2(1, 0);
61
    cout << ans;
62
    return 0;
63
}