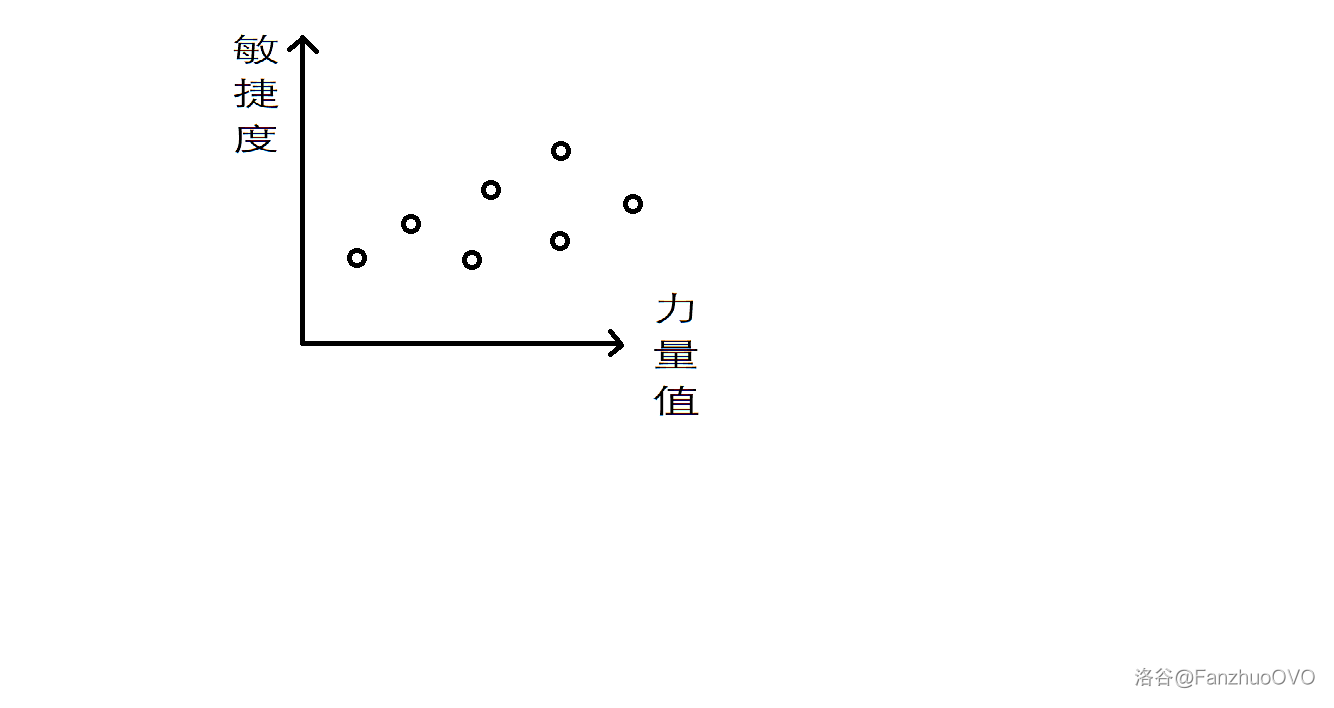
Problem Description#

Several robots are competing. Each robot has a strength and an agility value. During a match, if either of these values is greater than the opponent’s, it can eliminate the opponent. If one value is greater while the other is smaller, both robots are destroyed in mutual destruction. The goal is to arrange the order of robot matches such that all robots end up in mutual destruction. If possible, output TAK; otherwise, output NIE.

Approach#

First, sort the robots in ascending order by strength. After sorting, identify several paths from the lowest to the highest strength. 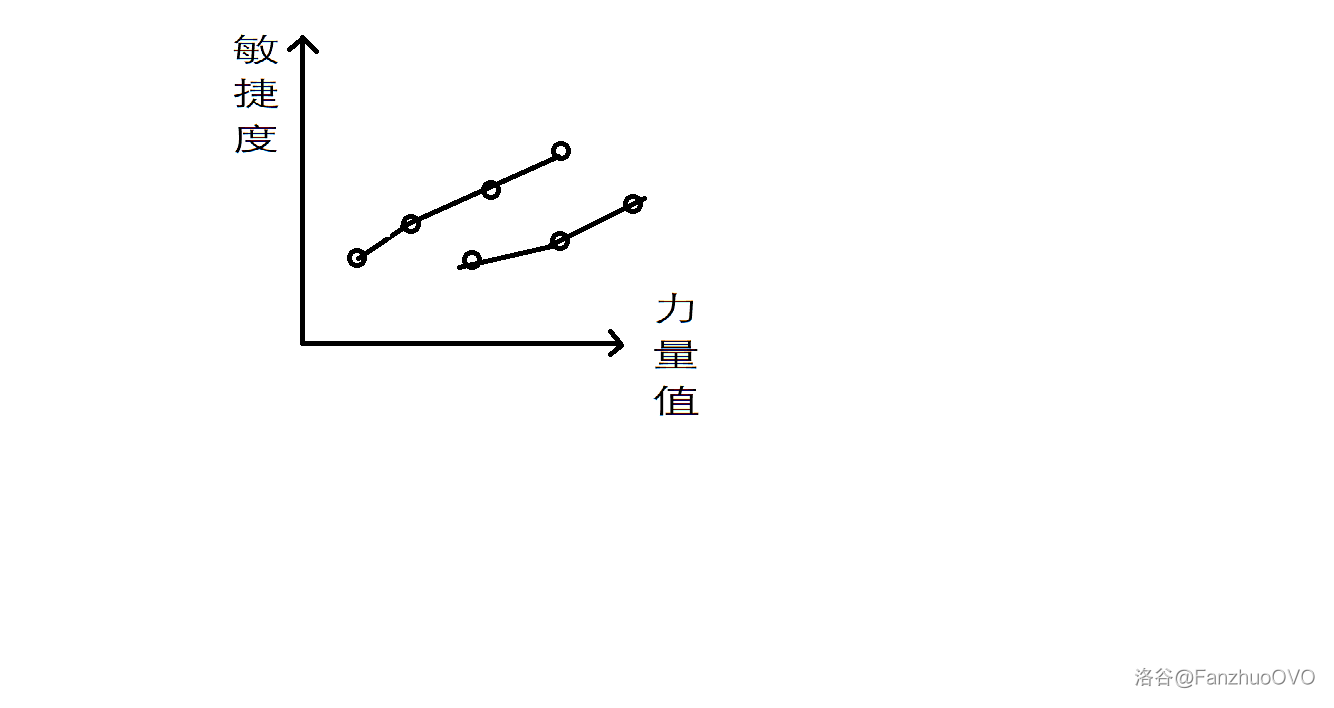This way, the endpoint of each path can “consume” others along the path, eventually leaving two expert robots that can mutually destroy each other, resulting in TAK.

Thus, we can conclude that if the number of paths is even, the answer must be TAK. But what if the number of paths is odd?

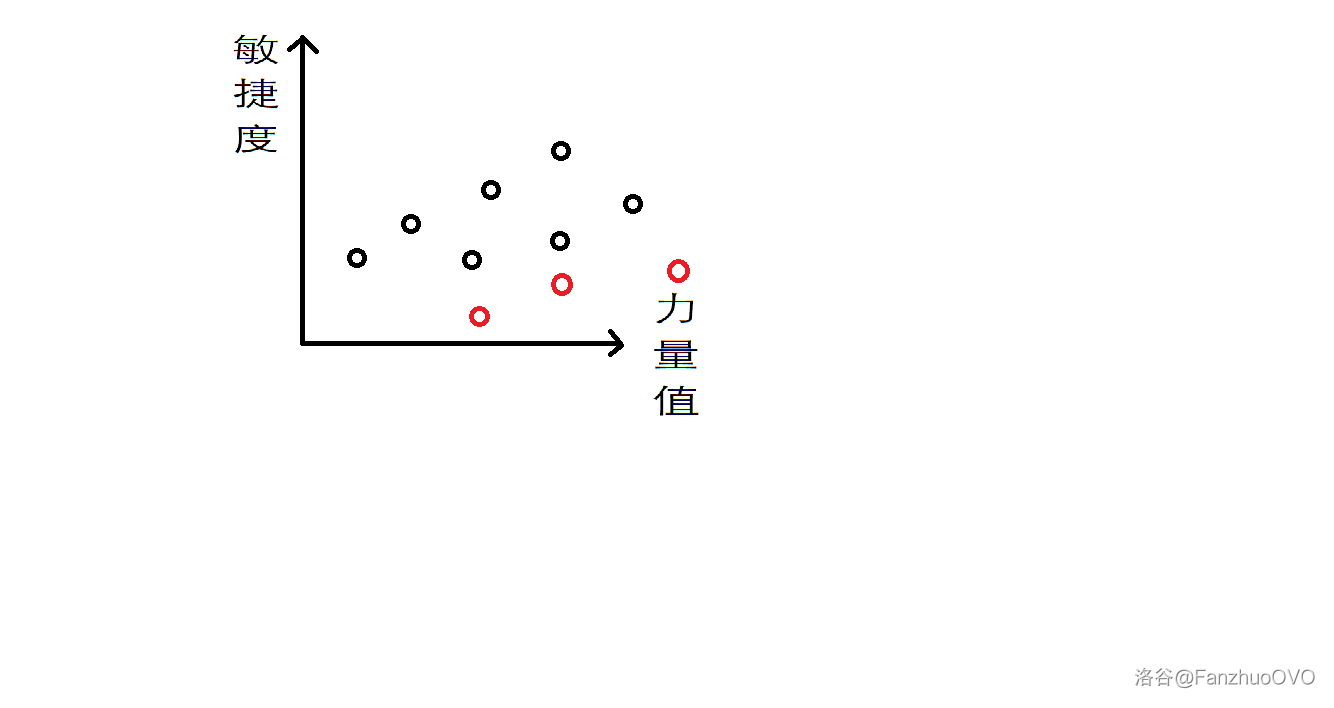
Given these robots, the paths would look like the following after identification:

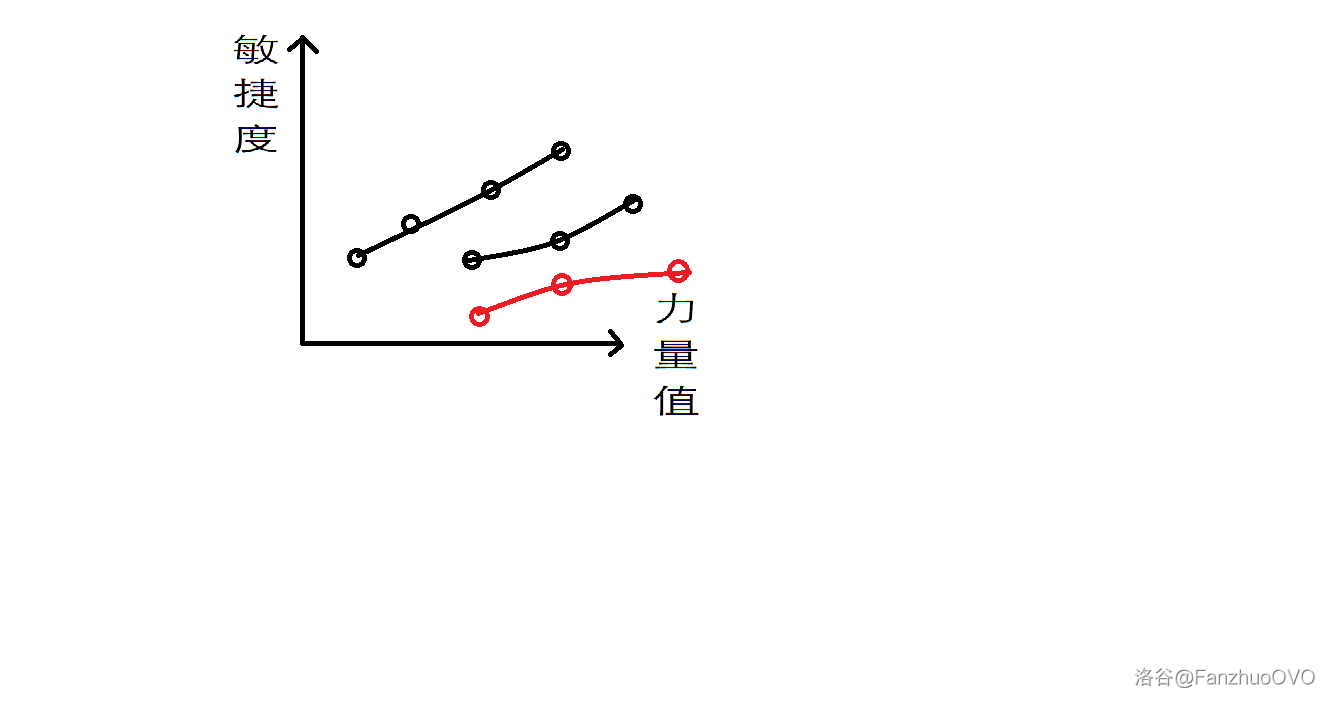
After “consumption,” an odd number of expert robots remain, which cannot mutually destroy each other.

However, it is actually possible.

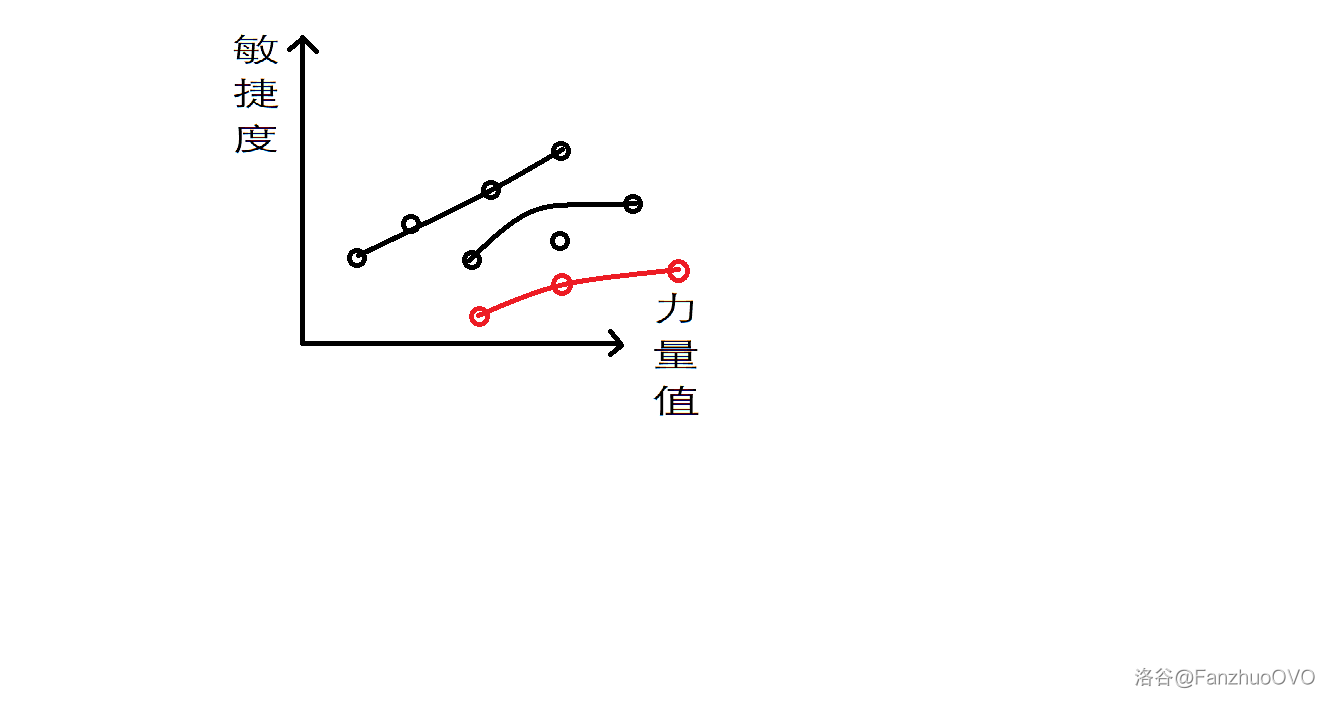
Have one expert robot skip a lesser robot it was supposed to “consume,” allowing it to finally mutually destroy with the extra expert robot (see the red path in the diagram).

If no such “lesser robot” can be found to trigger the expert robot’s mutual destruction, output NIE.

Done!

Thanks to purinliang for the guidance.