Explanation of Dijkstra’s Shortest Path Algorithm
Dijkstra’s algorithm was proposed by Dutch computer scientist Edsger W. Dijkstra in 1959, hence it is also called Dijkstra’s algorithm. It is an algorithm that finds the shortest paths from a single source vertex to all other vertices in a graph, solving the shortest path problem in weighted graphs. The main characteristic of Dijkstra’s algorithm is that it starts from the source vertex and adopts a greedy strategy, each time traversing to the adjacent nodes of the unvisited vertex with the smallest distance from the source, until it reaches the destination.
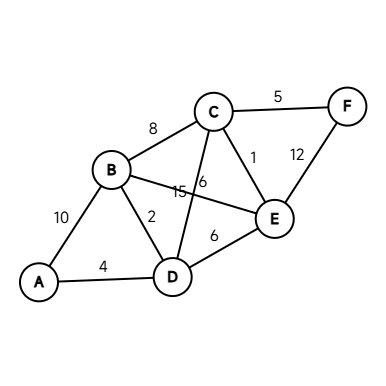
It’s quite simple to understand. Let’s take an example: we’ll use the multi-node, multi-path graph below to explain the process of Dijkstra’s algorithm finding the shortest path. (This graph might be a bit unclear; the distance between B and E is 6, and between C and D is 15. The numbers in this graph… qwq)

As you can see, starting from A, the points that can be reached directly are B and E. We then consider the distance from A to all other points as infinity (0x3F3F3F3F3F3F3F3F), and the distance from each point to itself as 0.
So, at the very beginning, the distances from A to each point are as follows.
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 10 (A-B) | Infinity | 4 (A-D) | Infinity | Infinity |
OK! Next, we find a point, other than A, with the shortest distance to A. Clearly, it’s D, right? So, the current optimal path is A-D. We use the distance of A-D to update the other points, which gives:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 (A-D-B) | 19 (A-D-C) | 4 | 10 (A-D-E) | Infinity |
Take the minimum of the distances from A to each point from the two tables, resulting in:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 (A-D-B) | 19 | 4 | 10 | Infinity |
Then we ignore A and D (these two points are already processed). It can be seen that the current optimal path is A-D-B. We use the distance of A-D-B to update the other points, which gives:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 14 (A-D-B-C) | 4 | 12 (A-D-B-E) | Infinity |
Again, take the minimum compared to the previous values:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 | 6 | 14 | 4 | 10 | Infinity |
We just need to repeat these steps. The final result will be:
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 0 (A-A) | 6 (A-D-B) | 11 (A-D-E-C) | 4 (A-D) | 10 (A-D-E) | 16 (A-D-E-C-F) |
